Heal

Σωστά.

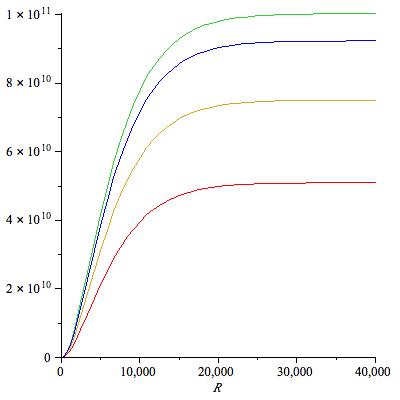
Δεν συμφωνώ. Τον τύπου που ζήτησες τον πήρες από την πρώτη απάντηση -και στην αρχική μορφή του και στο ολοκλήρωμα και στο διάγραμμα. Δεν είναι θέμα IQ είναι θέμα του πόσο έχει ξετρίψει κανείς με τους τύπους και τα διάγραμματα, όπως σε οτιδήποτε γενικά. Απλά είναι σημαντικό να δούμε τί ακριβώς σημαίνει το κάθε τί πριν προχωρήσουμε στο επόμενο βήμα. Λοιπόν όταν τραβάς τη γραμμή στα 5000 pc, όταν πέφτεις στην πράσινη καμπύλη αντιστοιχεί σε ένα κύλινδρο ύψους 5000 pc, όταν θα πέσεις στην μπλε μετράς πόσα αστέρια είναι στον κύλινδρο ύψους 1000 pc, η κίτρινη για 500 pc και η κόκκινη για 250 pc (όλοι οι κύλινδροι έχουν την ίδια ακτίνα 5000 pc στην προκειμένη περίπτωση). Για παράδειγμα αν σε απασχολεί ο αριθμός των άστρων που βρίσκονται σε ένα κύλινδρο ύψους 1000 pc και ακτίνας 10000 pc πας στον οριζόντιο άξονα σε ακτίνα 10000 pc και βλέπει που κόβει την μπλε καμπύλη, περίπου 8x10^10 αστέρια.

Το κέντρο μιας πόλης έχει πυκνότητα 100 κατοίκους αν στρέμμα και συνολική επιφάνεια 1000 στρέμματα. Τα περιχωρα της πολης έχουν πυκνότητα 1 κάτοικο ανα στρέμμα και συνολική επιφάνεια 10,000 στρέμματα. Οι κάτοικοι του κέντρου είναι 100,000, οι κάτοικοι όλου του οικιστικού συνόλου είναι 100,000 + 10,000=110,000. Αν παραστήσουμε με ένα διάγραμμα πόσοι κάτοικοι ζουν σε μια δεδομένη ακτίνα από το κέντρο της πόλης, το διάγραμμα αυτό θα αυξάνει πάντα, πιο γρήγορα θα αυξάνει εκεί που η πυκνότητα είναι μεγάλη. Δε θα μειώνεται όμως ποτέ και όταν βγούμε έξω από τα προάστεια θα σταθεροποιηθεί στην συνολική τιμή 110,000. Ακριβώς αυτό το νόημα έχουν τα διαγράμματα που σου έστειλα. Αν δε συμφωνήσουμε στα απλά δεν έχει κάποιο κέρδος να προχωρήσουμε στα πιο σύνθετα. Θα σου πρότεινα να μην ασχοληθείς με τον μαθηματικό τύπο, αλλά να λάβεις τις τιμές που θέλεις από το διάγραμμα.

Όχι δε θα έπρεπε να πέφτει. Πρόκεται για τον αριθμό των άστρων εντός ενός κυλίνδρου. Ο μεγαλύτερος κύλινδρος θα περιέχει τον μικρότερο κύλινδρο μέσα του κατά συνέπεια ο αριθμός των άστρων του μεγαλύτερου κυλίνδρου είναι μεγαλύτερος ή ίσος (στην οριακή περίπτωση που η συγκέντρωση πέφτει ραγδαία με την ακτίνα) από τον αριθμό των άστρων του μικρότερου κυλίνδρου.

Για να μην ταλαιπωρείς τα κομπιουτεράκια Ο αριθμός των άστρων (κατακόρυφος άξονας) που περιέχεται σε ένα κύλινδρο ακτίνας R (οριζόντιος άξονας), και ύψους z (η πράσινη καμπύλη αντιστοιχεί σε z=5000, η μπλε z=1000, η κίτρινη z=500, η κόκκινη z=250). Ο νορμαλισμός έχει επιλεγεί έτσι ώστε ο συνολικός αριθμός να είναι 10^11. Όλες οι αποστάσεις σε παρσεκ.

Φίλε μου, μάλλον το κουράζομουμε πολύ. Δες το συνημμένο αρχείο στο προηγούμενο μήνυμα και δες που τείνει για R και z στο άπειρο, αλλά μην αντικαταστήσεις κάποια τιμή στο n0, oπότε θα πάρεις εναν αριθμό που θα πολλαπλασιάζει το n0. Θέσε αυτό ίσο με τον αριθμό των άστρων που υποτίθεται ότι έχει ο Γαλαξίας. Τότε θα πάρεις την κατάλληλη τιμή του n0.

Στο ολοκλήρωμα που σου έγραψα παραπάνω υπάρχει μια σταθερά, την οποία παρέλειψα. Επειδή είναι αρκετά μεγάλος o τελικός τύπος τον παραθέτω ως συνημμένο αρχείο.formula.pdf

To θέμα κλειδώνεται προσωρινά το έχουν αναλάβει οι moderators.

Σε καταλαβαίνω και χαίρομαι που συνεννοούμαστε... Και όπως βλέπεις θέλει αρκετή "προπόνηση" για να ξεφύγει κανείς από τις κακοτοπιές, να βρει και να ερμηνεύσει τα νούμερα. Ελεύθεροι άνθρωποι είμαστε και ο καθένας μπορεί να ασχολείται με αυτό που τον ευχαριστεί. Αφού θέλεις να μπεις σε λίγο πιο βαθιά νερά κοίταξε αυτό το πολύ ενδιαφέρον (και ελπίζω προσιτό) άρθρο: http://arxiv.org/pdf/astro-ph/0401024v1 Συζητάει το ποια είναι η κατοικήσιμη ζώνη στο Γαλαξία υπό τις εξής προϋποθέσεις: 1. Παρουσία αστεριού που θα φιλοξενεί το ηλιακό σύστημα. 2. Αρκετά βαριά στοιχεία για τη δημιουργια πλανητών. 3. Αρκετός χρόνος για την βιολογική εξέλιξη. 4. Απουσία κοντινών υπερκαινοφανών που θα θέσουν σε κίνδυνο την ζωή εφόσον αυτή δημιουργηθεί. Δυστυχώς η βιβλιογραφία σε πρωτότυπες δημοσιεύσεις είναι αποκλειστικά στα Αγγλικά.

Όχι, η μέση απόσταση είναι το αντίστροφο της κυβικής ρίζας της πυκνότητας (0.0000022835)^(-1/3)~76 έτη φωτός. Άρα πρέπει να πάμε περίπου 76 έτη φωτός μακριά για να βρούμε το κοντινοτερο αστέρι. Γιατί ισχύει αυτό με την κυβική ρίζα, ας κάνουμε μια επαλήθευση. Αν η μέση απόσταση είναι 76 έτη φωτός, σε ένα όγκο (76 x 76 x 76) θα υπάρχει ένα αστέρι, άρα η πυκνότητα θα είναι 1/(76 x 76 x 76)=1 άστερι / 439000 κυβικά έτη φωτός =0.00000227 αστέρι/κυβικό έτος φωτός. (Χρησιμοποίησα απευθείας το αποτέλεσμά σου 0.0000022835 αστέρι ανά κυβικό έτος φωτός, υποθέτω πως δεν υπάρχει αριθμητικό λάθος). Με καλή πρόθεση γράφω ό,τι γράφω -και όπως βλέπεις κάθομαι και κάνω και τις πράξεις- απλά πολύ φιλικά το λέω και πάλι, ένας μαθηματικός τύπος είναι ένα εργαλείο που αποκτά αξία όταν μπορεί να συνδεθεί με ένα αποτέλεσμα το οποίο περιγράφει την φυσική πραγματικότητα. Αυτό απαιτεί κάποια εξάσκηση στα μαθηματικά και τη φυσική, η οποία πρέπει να προηγηθεί της χρήσης του τύπου. Αλλιώς κάθε τύπος θα δημιουργεί περισσότερες απορίες από αυτές που θα λύνει, όπως τώρα καλή ώρα. Το ότι παίρνει ένα εξάμηνο για να γίνει ένα μάθημα ανάλυσης και ολοκληρωμάτων στο πανεπιστήμιο σημαίνει πως όσο καλή διάθεση και να υπάρχει, δεν είναι εύκολο σε λίγες μέρες να κατακτήσει κανείς αυτές τις έννοιες και επιπλέον αυτά τα μαθήματα γίνονται στο πρώτο έτος ώστε να αποκτήσει κανείς το απαραίτητο υπόβαθρο.

...

Ολοκληρώνεις (η αντίστροφη διαδικασία από την παραγώγιση) και παίρνεις το συνολικό αριθμό. Το διάστημα που πρέπει να ολοκληρώσεις για να βρεις την απάντηση που ψάχνεις πρέπει να φτάσει μέχρι την απόσταση Rmax=16000, ενώ για το ύψος zmax, δεν έχει μεγάλη σημασία πόσο θα είναι, αρκεί ξεπεράσεις 2-3 φορές τις αποστάσεις za, zb. Κοίταξε λίγο το νούμερο που παίρνεις για το σημείο (8000, 8000) δεν βρίσκω το ίδιο όταν αντικαθιστώ σε αυτόν το τύπο, το αποτέλεσμα που παίρνω είναι 0.000035 άστρα ανά κυβικό έτος φωτός, δηλαδή μιας και έχουμε βγει από το Γαλαξιακό επίπεδο η πυκνότητα είναι πολύ μικρή. Για τη γειτονιά του Ήλιου (z ~ 0, R ~ 25000) παίρνω περίπου 0.002 άστρα ανα κυβικό έτος φωτός και μέση απόσταση περίπου 8 έτη φωτός, αριθμός που είναι στη σωστή τάξη μεγέθους, αν λάβουμε υπόψιν μας ότι το πλησιέστερο αστέρι είναι περίπου στα 4 έτη φωτός, Oύτως ή άλλως δίνει μια ενδεικτική τιμή και προφανώς ο γαλαξίας δεν έχει ομογενή πυκνότητα σε όλα τα σημεία που χαρακτηρίζονται από το ίδιο R και z. Y.Γ. Για να μπορέσεις να υπολογίσεις αυτά που θέλεις χρειάζεται γνώση μαθηματικών λυκείου και ίσως πιο προχωρημένων (ολοκληρώματα - κυλινδρικές συντεταγμένες) τα οποία δυστυχώς δεν μπορούν να επεξηγηθούν από το φόρουμ εύκολα.

Ας μείνουμε κατ'αρχήν εντός θέματος. Μια οποιαδήποτε λάμπα αν φωτίζει τον ουρανό τότε φωτορρυπαίνει, το αν είναι φθορισμού, αλογόνου ή πυρακτώσεως δεν προκαλεί ουσιαστικές διαφορές.

Υπάρχει κάποιο αριθμητικό λάθος στις πράξεις, μάλλον δεν έχεις βάλει αρνητικά πρόσημα στα εκθετικά. Το e είναι όντως είναι 2.71828, πάτησα το διπλανό πλήκτρο γράφοντας μάλλον... Ο τύπος μετασχηματίζεται αν αναφερθούμε σε έτη φωτός στην παρακάτω μορφή (για το n0 έχω θεωρήσει 1 άστρο αν κυβικό παρσέκ που είναι σύμφωνο με την εκτίμηση 0.02 άστρα ανά κυβικό έτος φωτός) Αν δώσεις την τιμή (1,1), τότε ο τύπος θα σου δώσει: 0.02* [e^(-1/1000)+ 0.02 * e^(-1/4500) ]* e^(-1/11000) ίσο περίπου με 0.02 (επειδή η ακρίβεια με την οποία γνωρίζουμε τις παραμέτρους είναι μικρή δεν αλλάζει κάτι ουσιαστικά αν στρογγυλοποιήσουμε). Ο αριθμός 0.02 αστέρια/κυβικό έτος φωτός, σημαίνει ότι η μέση απόσταση είναι η κυβική ρίζα αυτού του αριθμού: περίπου 0.3 έτη φωτός η μέση απόσταση ανάμεσα σε δυο αστέρια.

Η κατανομή των άστρων στο Γαλαξία μας είναι αρκετά ξεκάθαρη. Τώρα τα πράγματα που δεν είναι ξεκάθαρα είναι κατά πόσο το Ηλιακό μας Σύστημα είναι τυπική περίπτωση ηλιακού συστήματος. Το δεύτερο που αγνοούμε πλήρως είναι αν υποθέσουμε ότι ένας πλανήτης βρίσκεται στις "κατάλληλες" συνθήκες πόσο πιθανό είναι να αναπτυχθεί ζωή, με οποιαδήποτε μορφή. Υπάρχουν γενικά πολλές τέτοιες μελέτες που έχουν δημοσιευθεί και υπολογίζουν αυτές τις πιθανότητες κάνοντας υποθέσεις εργασίας. Αρκετό υλικό υπάρχει (στα αγγλικά) σε αυτή την σελίδα: http://www.astrobio.net/

n(R,z)=n0(exp(-z/za)+0.02 exp(-z/zb))exp(-R/hR). n(R,z)=n0*[ e^(-z/za) + 0.02*e^(-z/zb) ] * e^(-R/hR)

Οι σπείρες είναι στην ουσία κύματα πυκνότητας, δηλαδή ο ήλιος μας κάποια στιγμή μέσα στο γαλαξιακό έτος (250 εκατομμύρια χρόνια) περνάει από τις σπείρες και αυτό δε φαίνεται να τον εμπόδισε την ανάπτυξη της ζωής. Μια αναλογία που χρησιμοποιείται είναι η εικόνα των αυτοκινήρων που σταματούν στο φανάρι, αν κάποιος από ένα μπαλκόνι δει ένα στιγμιότυπο τότε θα δει πιο πολλά αυτοκίνητα κοντά στο φανάρι. Στο πέρασμα του χρόνου όμως δεν είναι τα ίδια αυτοκίνητα που είναι κολλημένα στο φανάρι, αλλά άλλα που σταματούν και αντικαθιστούν αυτά που φεύγουν. Εγώ ευχαριστώ για τα καλά σας λόγια

Υπάρχει το εξής θέμα αν θεωρήσουμε την περιοχή των 16.000 ετών φωτός ότι έχει μέση πυκνότητα ενός άστρου ανά κυβικό έτος φωτός, και ότι πρόκειται για μια σφαιρα τέτοιου σχήματος τότε καταλήγουμε στο τεράστιο νούμερο 5000 δις αστεριών, που είναι που είναι το πολλαπλάσιο από την εκτίμηση για όλα τα άστρα του Γαλαξία μας συνολικά (10^10). Άρα αυτός ο υπολογισμός μας δίνει πολύ μεγαλύτερα αποτέλεσμα. Στην ουσία αν κάνουμε ένα διάγραμμα της πυκνότητας θα πρέπει να έχουμε υπόψιν μας ότι πρόκειται για ένα λεπτό δίσκο. Ο δίσκος αυτός αποτελείται στην ουσία από δύο πληθυσμούς που μειώνονται όσο απομακρυνόμαστε από την κέντρο του Γαλαξία και παραμένουμε στο οριζόντιο επίπεδο αλλά και καθώς απομακρυνόματε από το οριζόντιο επίπεδο (δηλαδή και στην κατεύθυνση R και z). Η μείωση αυτή μπορεί να περιγραφεί από έναν εκθετικό νόμο, δηλαδή ο η πυκνότητα υποδιπλασιάζεται όταν διανύσουμε μια δεδομένη απόσταση. Αν έχεις μια άνεση με τους μαθηματικούς τύπους τότε η πυκνότητα των άστρων ανά κυβικό παρσεκ στο σημείο (R, z), όπου z η απόσταση από το Γαλαξιακό επίπεδο και R η προβολή της συνολικής απόστασης πάνω στο Γαλαξιακό επίπεδο (στην ουσία πρόκειται για τις γνωστές κυλινδρικές συντεταγμένες) δίδεται από τον εξής τύπο: n(R,z)=n0(exp(-z/za)+0.02 exp(-z/zb))exp(-R/hR). Τι σημαίνει τώρα αυτός ο μαθηματικός τύπος: Ο αστρικός πληθυσμός του Γαλαξία μας μπορεί να περιγραφεί ως το άθροισμα δύο πληθυσμών που ο κάθε ένας περιγράφεται από έναν εκθετικό νόμο. Κατ'αρχήν υπάρχει ένας πληθυσμός με πυκνότητα n0 κοντά στο κέντρο του γαλαξία ο οποίος μειώνεται κατά "e" (η βάση των φυσικών λογαρίθμων, 2.81821) κάθε φορά δηλαδή που απομακρυνόμαστε "za" απόσταση από το κέντρο. Αντίστοιχα υπάρχει ένας πληθυσμός με πυκνότητα 0.02 φορές το n0 ο οποίος μειώνεται κατά "e" κάθε φορά που απομακρυνόμαστε zb αποσταση από το γαλαξιακό επίπεδο. Η πυκνότητα όμως πέφτει και για τους δυο πληθυσμούς ακόμη και αν μένουμε στο γαλαξιακό επίπεδο και κινούμαστε μακριά από το κέντρο, αυτή μειώνεται κατά "e" κάθε φορά απο απομακρυνόμαστε "hR" από το κέντρο. Οι αριθμητικές τιμές είναι n0=0.02 pc^(-3) (για αυτό τον αριθμό έχω κάποιες επιφυλάξεις, μου φαίνεται κάπως μικρός αλλά τον αναφέρω όπως τον βρήκα στη βιβλιογραφία, κάτι περίπου στη μονάδα μου φαίνεται πιο λογικό και συνεπές με τα 10^10 αστέρια που υπάρχουν στο γαλαξία, αλλά πιθανόν να οφείλεται στο ότι ένα μεγάλο μέρος των αστεριών είναι μικρότερα σε μάζα από ότι ο ήλιος), za=325pc, zb=1400pc και hR=3500pc, όλες οι τιμές δίνονται σε parsec και αντιστοιχεί 1pc=3.26 έτη φωτός. Είναι σημαντικό να πούμε ότι αυτός ο τύπος περιγράφει τα γενικά χαρακτηριστικά και δεν μπορεί εύκολα να εφαρμοστεί σε συγκεκριμένες περιοχές, για παράδειγμα αν βρισκόμαστε στη γειτονιά ενός σμήνους είναι προφανές ότι θα υποτιμήσει τον αριθμό των άστρων όπως θα συμβεί και κοιτάζοντας τη γειτονιά του Ήλιου. Αν θέλουμε όμως να έχουμε μια εικόνα του τί συμβαίνει γενικά σε ακτίνα "R" και ύψος "z" είναι ικανοποιητικός. Επίσης επειδή ακόμη δε γνωρίζουμε τον αριθμό των άστρων στο Γαλαξία μας, όπως είδες είμαστε σίγουροι για την τάξη μεγέθους αλλά όχι για τον αριθμητικό παράγοντα που υπάρχει μπροστά, είναι πιθανόν νεότερες μελέτες να επανεκτιμήσουν τις παραπάνω αριθμητικές τιμές.

Ακριβώς, το θέμα είναι να μην είμαστε και πλεονέκτες. Κάτι το αγοράζεις ήδη φθηνότερα (-Α%) από την τυπική τιμή στην Ελλάδα, το δηλώνεις ως μεταχειρισμένο, γιατί τέτοιο είναι εφόσον έχει ανοιχθεί (-Β%), μετά να θελήσεις να γλιτώσεις ένα ακόμη Γ% για τους φόρους μου φαίνεται πως πάει πολύ...

Από χώρες εκτός Ευρωπαϊκής Ένωσης με έχουν σταματήσει δυο φορές στο τελωνείο, για τυχαίο έλεγχο, τη μια μου ζήτησαν να ανοίξω τη βαλίτσα μου. Την άλλη απλά με ρώτησαν αν έχω να δηλώσω τίποτα, τους είπα για φωτογραφική μηχανή και λαπτοπ, μου είπαν εντάξει και με ρώτησαν στη συνέχεια να έχω ποτά ή πούρα μαζί μου, τους είπα όχι και συνέχισα χαμογελαστός.

Εφόσον η δηλωμένη αξία είναι σε λογικά πλαίσια, στην τυπική τιμή του μεταχειρισμένου λογικά δε θα σε ενοχλήσει κανείς, αυτό είναι νόμιμο και, κατά τη γνώμη μου, ηθικό. Προφανώς ένα δέμα 50 κιλών με ένα τηλεσκόπιο μέσα δε θα πείσει αν το κοστολογήσεις στα 5 δολλάρια, μιας δηλώνεις την αξία του αντικειμένου στο ταχυδρομείο όταν το στέλνεις σε μια κάρτα που την κολλάνε πάνω στο δέμα, και τότε είναι πιθανόν να μπλέξεις -το οποίο είναι και νόμιμο και λογικό επίσης.

Χωρίς να είμαι 100% σίγουρος επιτρέπεται η εισαγωγή ατελώς ειδών για προσωπική χρήση ή δώρα αξίας μέχρι 430 Ευρώ. Αν κάτι κοστίζει παραπάνω πρέπει να δηλωθεί. Αυτό πάντως που είναι και νόμιμο και λογικό, είναι ότι ένα οποιοδήποτε προϊόν εντός κλειστής συσκευασίας έχει μια "Χ" τιμή η οποία αυτόματα μειώνεται από τη στιγμή που είναι εκτός συσκευασίας γιατί παύει πλέον να είναι καινούριο και αχρησιμοποιήτο.

Μια σημαντική παράμετρος που πρέπει να εξετάσεις είναι το βάρος και ο όγκος που σου επιτρέπει να πάρεις στο αεροπλάνο η εταιρεία με την οποία πετάς. Σε μερικές είναι μια αποσκευή βάρους 23 κιλών, σε άλλες είναι δύο, συνολικά 46 κιλά. Επίσης δες τί μπορείς να πάρεις μαζί σου στη χειραποσκευή, ευαίσθητα αντικείμενα για παράδειγμα, που θέλω να είμαι σίγουρος ότι δε θα κακοποιηθούν στο δρόμο. Για το τελωνείο δεν ξέρω ακριβώς τη διαδικασία, αλλά ποτέ δε μου έχουν δημιουργήσει θέμα όταν μεταφέρω είδη (όπως ο laptop, φωτογραφική μηχανή, φακούς κλπ), τα οποία έχω ήδη ανοίξει και δεν προορίζονται για μεταπώληση, αλλά για να τα χρησιμποιήσω εγώ.

Αν θελήσουμε να μη μπούμε πολύ βαθειά τότε η βασική ιδέα είναι η εξής. Αν έχουμε δύο σώματα σε τροχιά τότε αυτά θα διαγράφουν ελλείψεις γύρω από το κοινό κέντρο μάζας. Το κέντρο μάζας είναι κοντά στο σώμα με τη μεγαλύτερη μάζα και αν το ένα σώμα είναι πολύ μεγαλύτερη μάζα, τότε μπορούμε να θεωρήσουμε με καλή ακρίβεια ότι το μικρότερο περιφέρεται γύρω από το μεγαλύτερο. Οταν έχουμε περισσότερα σώματα τότε αυτά κινούνται γύρω από το κοινό κέντρο μάζας και η επίλυση των τροχιών είναι εξαιρετικά πιο πολύπλοκη, αλλά στο ηλιακό σύστημα που δεσπόζει ο Ήλιος το κέντρο μάζας του Ηλιακού συστήματος σχεδόν ταυτίζεται με τον Ήλιο. Αυτά τουλάχιστον μας λέει ο Νεύτωνας. Όποτε ένα ηλιακό σύστημα με τη Γη ακίνητη δε θα έβγαζε νόημα δυναμικά (θα έπρεπε να αρχίσουμε να προσθέτουμε υποθετικές δυνάμεις). Επιπλέον έχει παρατηρηθεί το φαινόμενο της αποπλάνησης του φωτός το οποίο μας επιβεβαιώνει το γεγονός ότι η τροχιακή κίνηση της Γης επιβεβαιώνεται και ως προς τα αστέρια που βρίσονται εκτός Ηλιακού συστήματος (είναι λίγο μακροσκελής εξήγηση του οπότε ρίξε μια ματιά εδώ: http://www.physics4u.gr/articles/2005/aberration1.html ). Κατά συνέπεια, εκτός από τον Ήλιο θα έπρεπε να αναγκάζαμε και το υπολοιπο Σύμπαν να γυρίζει γύρω μας. Όπως καταλαβαίνεις αυτό θα μας προκαλούσε μια τρομερή ζαλάδα... Αν θελήσουμε να πάμε πιο βαθειά, τότε μπαίνουμε σε άλλα κεφάλαια, ετοίμασε τα παυσίπονα μιας και θα μείνουμε εμείς ακίνητοι και θα αρχίσουν όλα να γυρίζουν... Με τη γενική θεωρία της σχετικότητας η περιγραφή του κόσμου επιτρέπεται σε οποιοδήποτε σύστημα αναφοράς, αδρανειακό ή μη -ο λόγος που προτιμάμε τον Ήλιο είναι οτι βρισκεται κοντά στο κέντρο μάζας οπότε είναι πιο κοντά στο ακίνητο σημείο. Αν θελήσουμε να περάσουμε σε ένα σύστημα αναφοράς με μια ακίνητη Γη και δεν έχουμε κάποιο λόγο να το απορρίψουμε εκ των προτέρων, με εξαίρεση την πολυπλοκότητά του. Τώρα για να συνοψίσουμε το θέμα, θεωρώντας το σύμπαν ισότροπο και ομογενές δεν μπορούμε να του αποδώσουμε μια συνολική περιστροφική κίνηση -γιατί θα εισήγαγε έναν άξονα ο οποίος θα έσπαζε τη συμμετρία η οποία οδηγεί στην ισοτροπία. Η ερώτηση στο αν η Γη κινείται γύρω από τον Ήλιο ή το αντίστροφο είναι αρκετά ξεκάθαρη, η Γη κινείται γύρω από τον Ήλιο (με βάση αυτό που εννούμε στην καθημερινή μας γλώσσα), τα βασικά επιχειρήματα: Το Ηλιακό σύστημα περιγράφεται πολύ απλούστερα με ελλείψεις γύρω από τον Ήλιο, παρά με επικύκλους γύρω από τη Γη. Δυναμικά είναι συνεπές με την Νευτώνεια περιγραφή, αν η κίνηση δεν ήταν γύρω από το κέντρο μάζας θα έπρεπε να το γεμίσουμε με υποθετικές δυνάμεις. Το φως από τα αστέρια υφίσταται αποπλάνηση οπότε υπάρχει κίνηση και ως προς αυτό το σύστημα αναφοράς. Η διαστημική εξερεύνηση πλέον έχει διαλύσει κάθε αμφιβολία. Η γενική σχετικότητα μας αλλάζει, όχι την ουσία των παρατηρήσεων, αλλά τον τρόπο περιγραφής. Δηλαδή μας λέει ότι μπορούμε να περιγράψουμε τον κόσμο σε όποιο σύστημα αναφοράς θέλουμε με το προφανές κόστος της εξαιρετικής πολυπλοκότητα.

Αν προσπαθήσω να μετασχηματίσω την αρχική ερώτησή: η απορία γενικά είναι έστω ότι έχουμε δύο σώματα σε τροχιά μεταξύ τους, ποιο είναι το ασφαλές κριτήριο με βάση το οποίο θα πούμε ότι το ένα γυρίζει γύρω από το άλλο (το Α γύρω απο το Β και όχι το Β γύρω από το Α); Υποψιάζομαι ότι η ερώτηση σχετίζεται και από την σχετική κίνηση δύο σωμάτων που κινούνται ευθύγραμμα ομαλά (σε ένα αδρανειακό σύστημα) και έχουμε το δικαίωμα να θεώρησουμε αυθαίρετα το κάθε ένα ακίνητο, μιας και αυτό που μετράει τελικά είναι η σχετική κίνηση; Οποτε τελικά ρωτάς γιατί να μην έχουμε σχετική "κυκλική κίνηση";